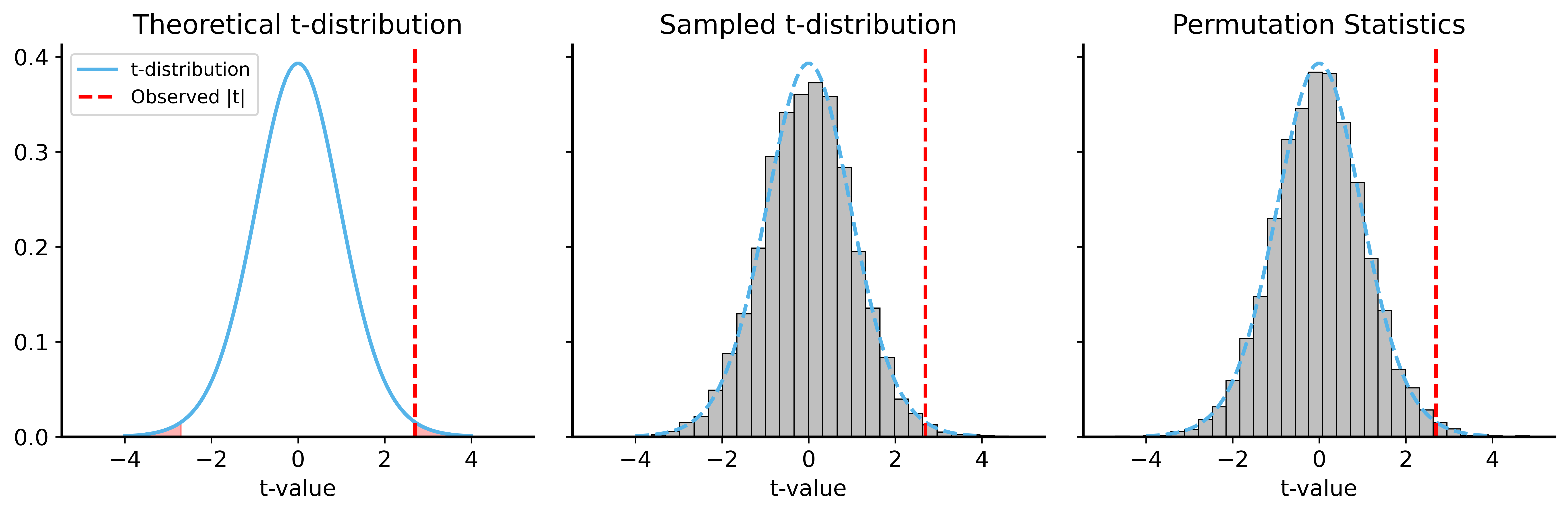
def permutation_test_t(x, y, num_permutations=10000, rng=None):
observed_stat = stats.ttest_ind(x, y, equal_var=True).statistic
combined = np.concatenate([x, y])
if rng is None:
rng = np.random.default_rng()
permuted_stats = []
for _ in range(num_permutations):
permuted = rng.permutation(combined)
x_perm = permuted[:len(x)]
y_perm = permuted[len(x):]
permuted_stat = stats.ttest_ind(x_perm, y_perm, equal_var=True).statistic
permuted_stats.append(permuted_stat)
permuted_stats = np.array(permuted_stats)
p_value = np.mean(np.abs(permuted_stats) >= np.abs(observed_stat))
return permuted_stats, p_value
permuted_stats, p_value_perm = permutation_test_t(samples_a, samples_b, rng=rng)
print(f"Permutation test p-value: {p_value_perm:.6f}")