Lecture 08: Linear Regression

Joseph Rudoler

2026-01-06

From Inference to Prediction

So far we’ve focused on inference:

  • Estimating parameters
  • Testing hypotheses
  • Quantifying uncertainty

Now: Prediction — using data to forecast outcomes

Predictions from Patterns

How do we make predictions?

  • Look for patterns in data
  • Use patterns to make informed guesses

Why not just memorize?

  • Memorization doesn’t generalize
  • We need predictions for new, unseen data

The Galton Dataset

Classic dataset: heights of parents and children

family father mother gender height kids male female
0 1 78.5 67.0 M 73.2 4 True False
1 1 78.5 67.0 F 69.2 4 False True
2 1 78.5 67.0 F 69.0 4 False True
3 1 78.5 67.0 F 69.0 4 False True
4 2 75.5 66.5 M 73.5 4 True False

The Simplest Prediction

Task: Predict height of a new child (no other information)

Solution: Use the average height!

Mean height: 66.76 inches

Distribution of Heights

Can We Do Better?

What if we have more information?

  • Child’s sex
  • Parents’ heights

If these are related to height, they should inform our prediction!

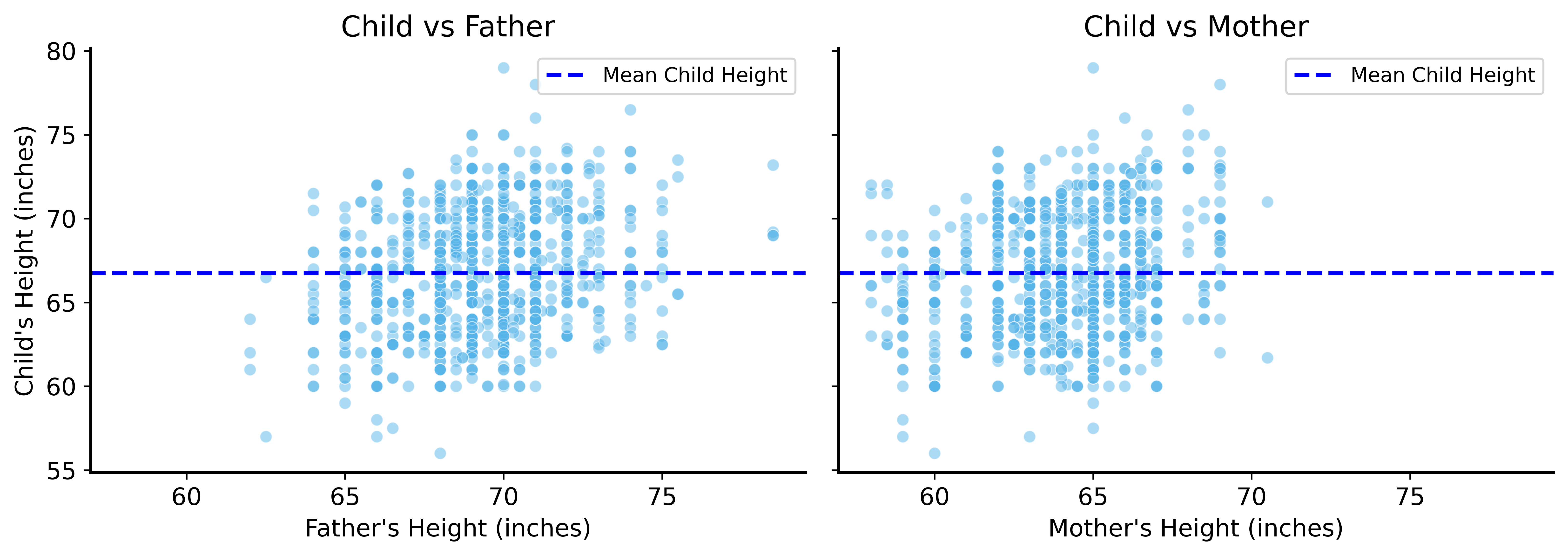
Child Height vs Parent Height

The Pattern

Taller parents → taller children (generally)

But how much taller?

We need to quantify this relationship.

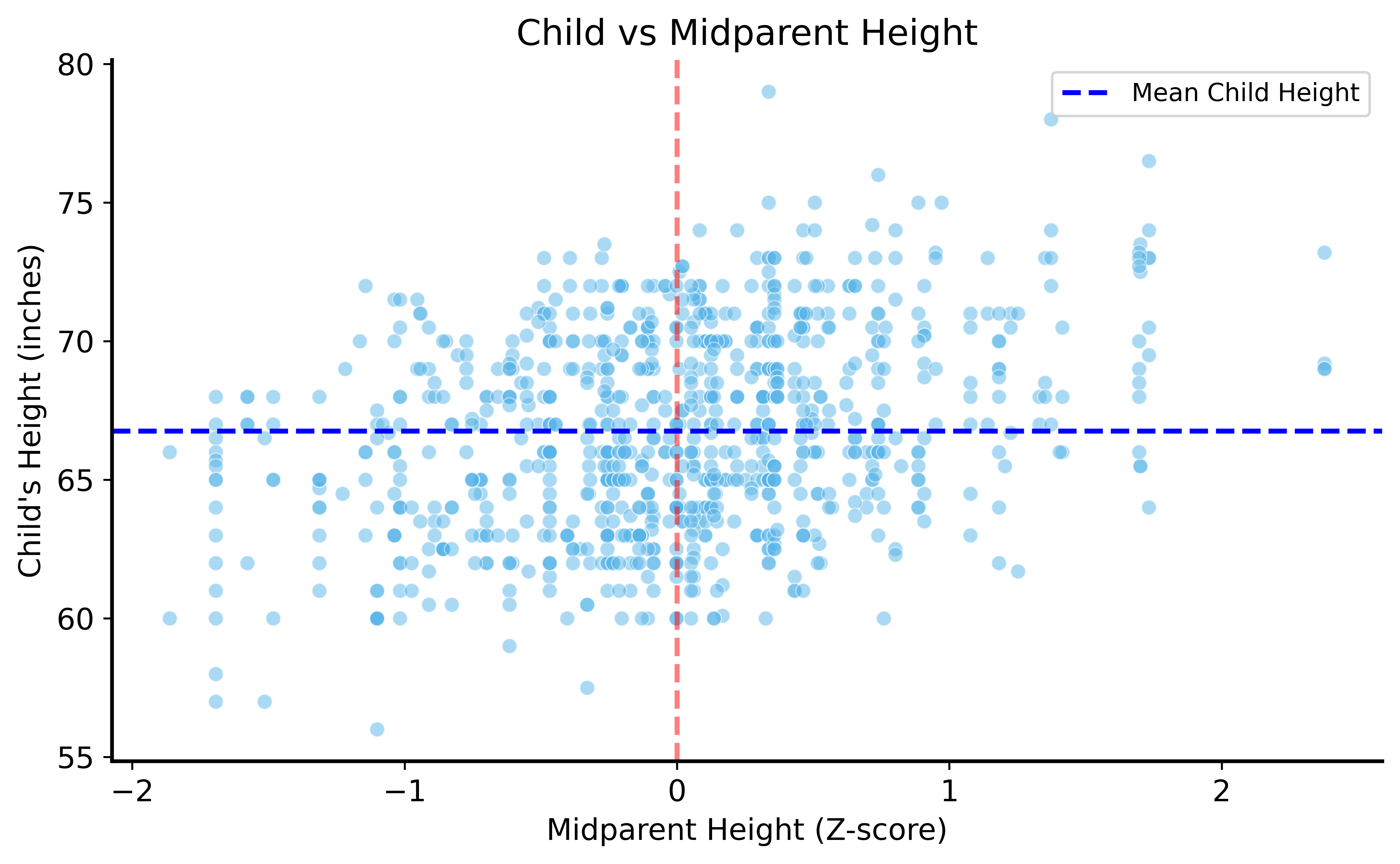
Combining Parent Heights

Problem: Father and mother heights are on different scales

Solution: Standardize (z-score) heights

\[z = \frac{\text{height} - \text{mean}}{\text{std dev}}\]

Then combine: midparent height = average of z-scores

Standardization

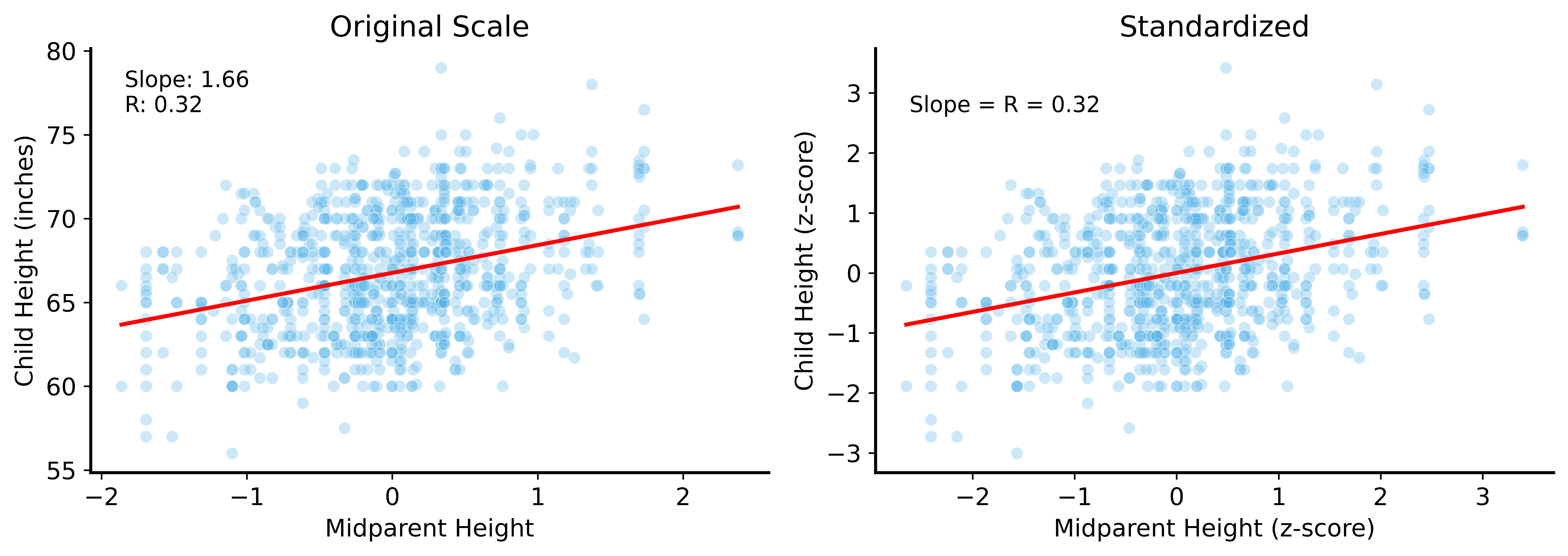
Child Height vs Midparent Height

Linear Regression

Model the relationship as a line:

\[\text{predicted height} = \text{slope} \times \text{midparent} + \text{intercept}\]

Ordinary Least Squares (OLS): Find the line that minimizes squared errors

\[\text{minimize } \sum_i (\text{predicted}_i - \text{actual}_i)^2\]

Why Squared Errors?

  1. No cancellation of positive/negative errors
  2. Larger errors are penalized more heavily
  3. Mathematically convenient (differentiable)

Fitting the Model

Code 
model = ols("height ~ midparent", data=galton).fit()
predicted_heights = model.predict(galton["midparent"]).values
print(f"Intercept: {model.params['Intercept']:.2f}")
print(f"Slope: {model.params['midparent']:.2f}")
Intercept: 66.77
Slope: 1.66

Visualizing the Fit

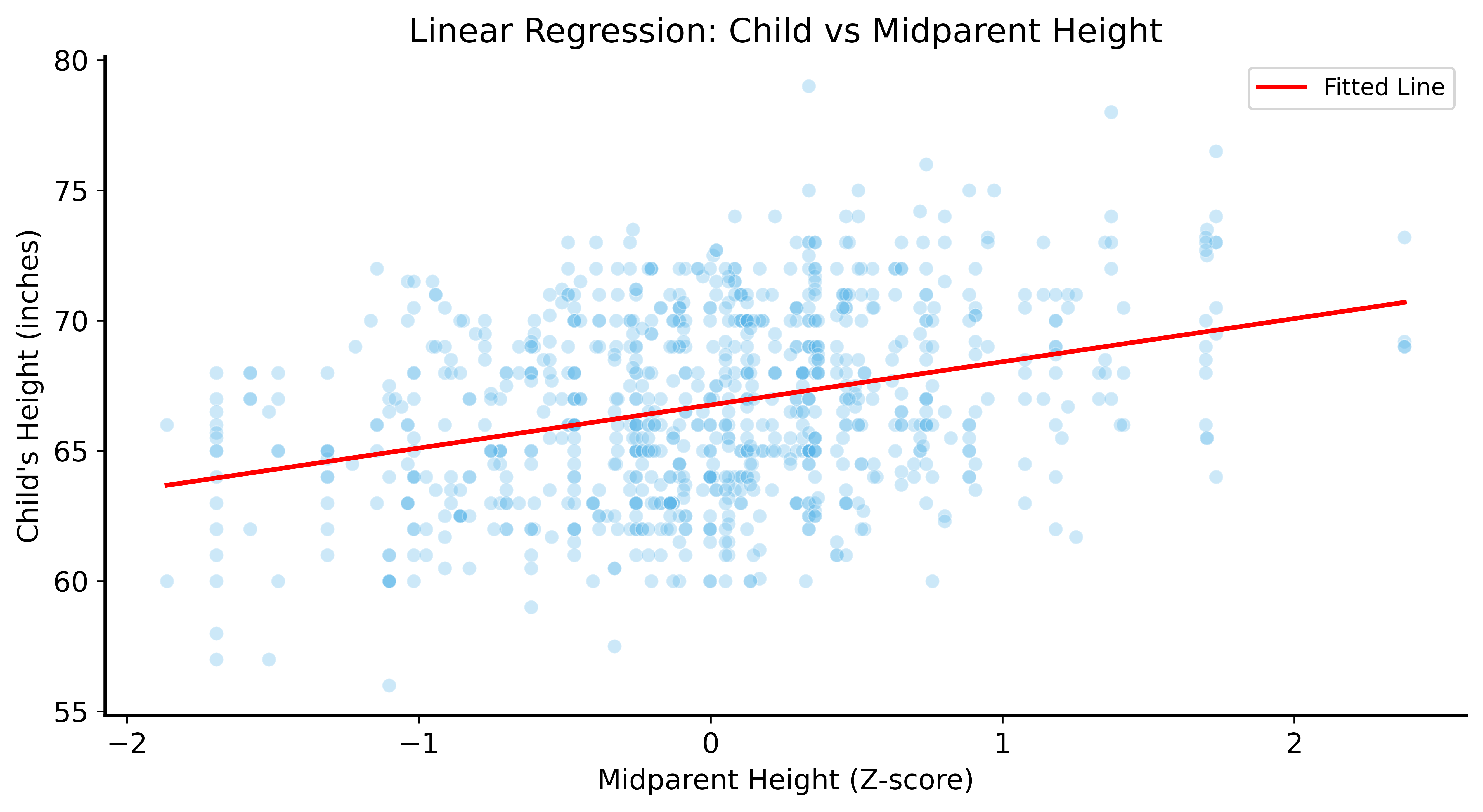
Interpreting the Slope

Slope ≈ 1.7

Interpretation: For every 1 standard deviation increase in midparent height, predicted child height increases by 1.7 inches.

Prediction Errors (Residuals)

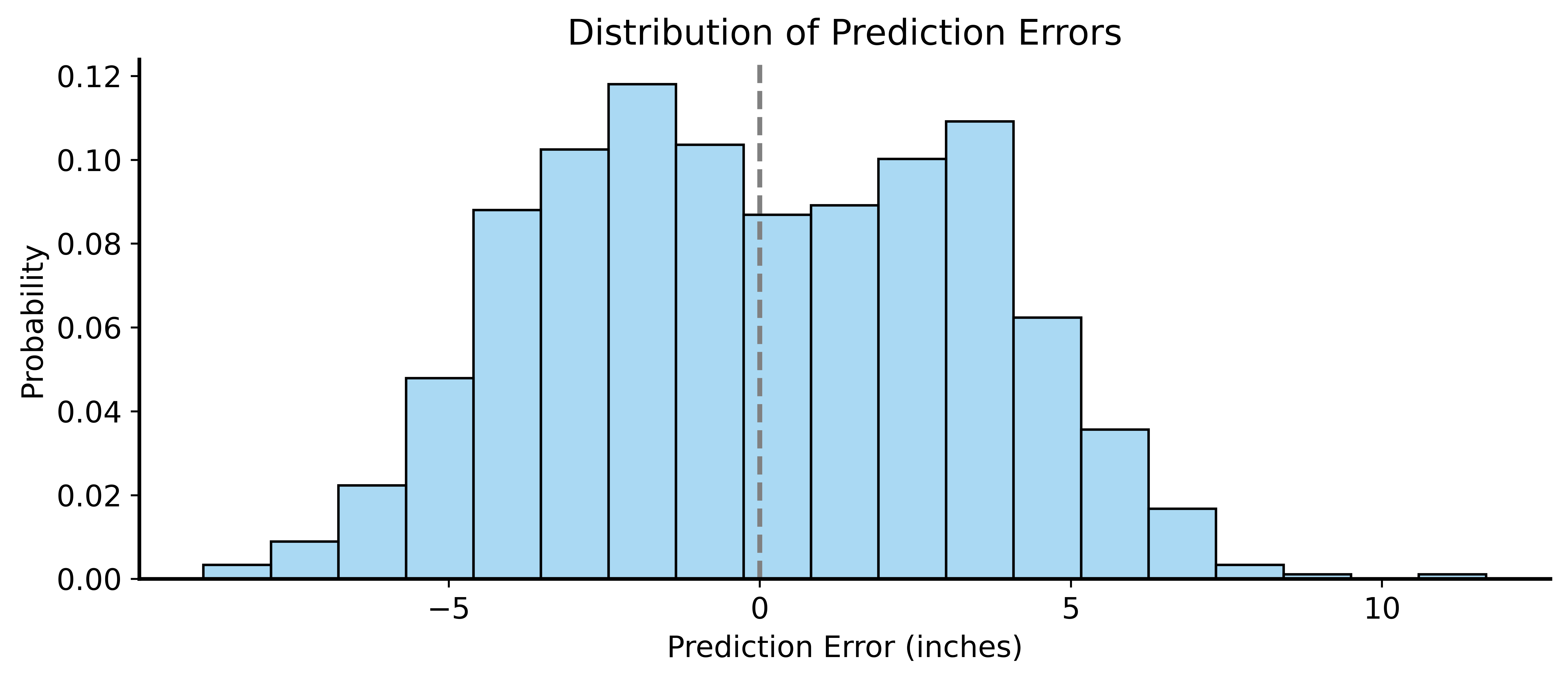
Evaluating Predictions

Code 
print(f"Mean error: {np.mean(errors):.2e}")
print(f"Root Mean Squared Error: {np.sqrt(np.mean(errors**2)):.2f} inches")

# Compare to naive prediction
naive_rmse = np.sqrt(np.mean((galton["height"] - mean_height) ** 2))
print(f"Naive RMSE (just use mean): {naive_rmse:.2f} inches")
Mean error: -2.43e-14
Root Mean Squared Error: 3.39 inches
Naive RMSE (just use mean): 3.58 inches

Using parent info improves predictions! (3.39 vs 3.58 inches)

The Probabilistic View

Notice: residuals are approximately normal!

This motivates the probabilistic regression model:

\[Y \sim \mathcal{N}(\beta_0 + \beta_1 X, \sigma^2)\]

The response \(Y\) is a random variable with:

  • Mean that depends on \(X\)
  • Inherent variability \(\sigma^2\)

Uncertainty in Regression

Because \(Y\) is random:

  • Different samples → different estimates of \(\beta_0\), \(\beta_1\)
  • Need to quantify uncertainty (next lecture!)

Correlation

Correlation coefficient (\(r\)): measures linear relationship strength

Value Interpretation
\(r = 1\) Perfect positive correlation
\(r = -1\) Perfect negative correlation
\(r = 0\) No linear relationship

Correlation = Standardized Slope

Key insight: When both variables are standardized, the slope equals the correlation!

\[r = \text{slope when } X \text{ and } Y \text{ are z-scored}\]

Demonstration

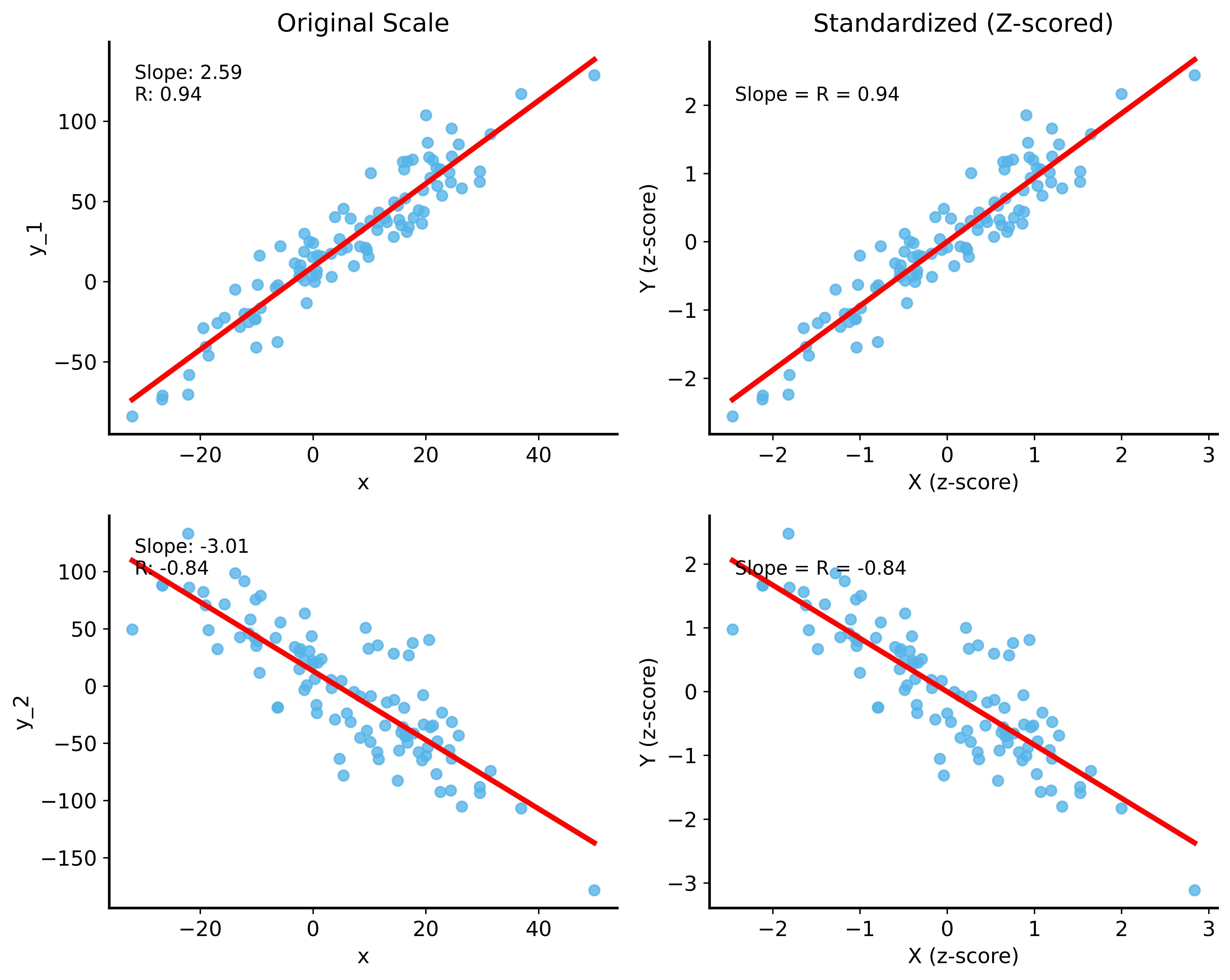
Galton Data: Correlation

Summary

Linear Regression

  • Model relationships as linear equations
  • OLS finds the best-fitting line
  • Slope quantifies the relationship

Correlation

  • Measures linear relationship strength
  • Equals slope when variables are standardized

Probabilistic Interpretation

  • \(Y\) is a random variable
  • Regression estimates expected value given \(X\)

Next Time

Regression Inference and Multiple Regression

  • Hypothesis tests for regression coefficients
  • Confidence intervals for predictions
  • Multiple predictors simultaneously