Lecture 09: Regression Inference and Multiple Regression
2026-01-06
Recap: Linear Regression
\[Y = \beta_0 + \beta_1 X + \epsilon\]
- \(\beta_0\): intercept
- \(\beta_1\): slope
- \(\epsilon\): error term (random noise)
We use data to estimate \(\hat{\beta}_0\) and \(\hat{\beta}_1\)
Sampling Variability in Regression
Different samples → different estimates of \(\beta\)
This is the same sampling variability we’ve discussed throughout the course!
Hypothesis Testing in Regression
Common question: Is there a relationship between \(X\) and \(Y\)?
Hypotheses:
- \(H_0\): \(\beta_1 = 0\) (no relationship)
- \(H_1\): \(\beta_1 \neq 0\) (there is a relationship)
Simulating the Null Distribution
How can we generate \(\hat{\beta}_1\) values under \(H_0\)?
Permutation test: Shuffle \(Y\) values to break the \(X\)-\(Y\) relationship
Permutation Test for Regression
Code
def permutation_test_regression(data, x_col, y_col, n_permutations=1000, rng=None):
if rng is None:
rng = np.random.default_rng()
# Observed slope
model = smf.ols(f'{y_col} ~ {x_col}', data=data).fit()
observed_beta = model.params[x_col]
# Permutation distribution
perm_betas = []
for _ in range(n_permutations):
y_perm = rng.permutation(data[y_col])
perm_model = smf.ols(f'{y_col} ~ {x_col}',
data=data.assign(**{y_col: y_perm})).fit()
perm_betas.append(perm_model.params[x_col])
perm_betas = np.array(perm_betas)
p_value = np.mean(np.abs(perm_betas) >= np.abs(observed_beta))
return observed_beta, perm_betas, p_value
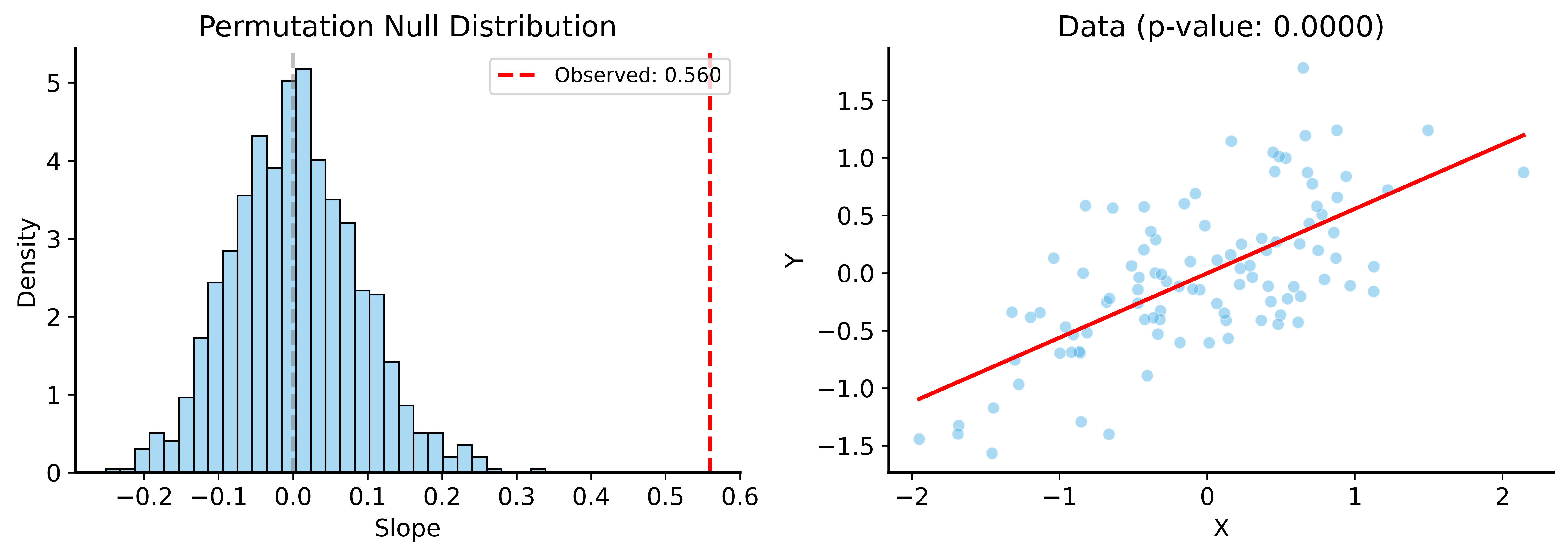
Example
Observed slope: 0.5596
Permutation p-value: 0.0000
Permutation vs Parametric
Parametric Results Match!
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.443
Model: OLS Adj. R-squared: 0.437
No. Observations: 100 F-statistic: 77.87
Covariance Type: nonrobust Prob (F-statistic): 4.29e-14
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -0.0023 0.049 -0.047 0.962 -0.100 0.095
x 0.5596 0.063 8.824 0.000 0.434 0.685
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Confidence Intervals for Regression
Use bootstrap to estimate CI for slope:
Code
def bootstrap_regression_ci(data, x_col, y_col, n_bootstraps=1000, alpha=0.05, rng=None):
if rng is None:
rng = np.random.default_rng()
n = len(data)
coefs = []
for _ in range(n_bootstraps):
sample = data.sample(n, replace=True)
model = smf.ols(f"{y_col} ~ {x_col}", data=sample).fit()
coefs.append(model.params[x_col])
coefs = np.array(coefs)
lower = np.percentile(coefs, 100 * alpha / 2)
upper = np.percentile(coefs, 100 * (1 - alpha / 2))
return coefs, lower, upper
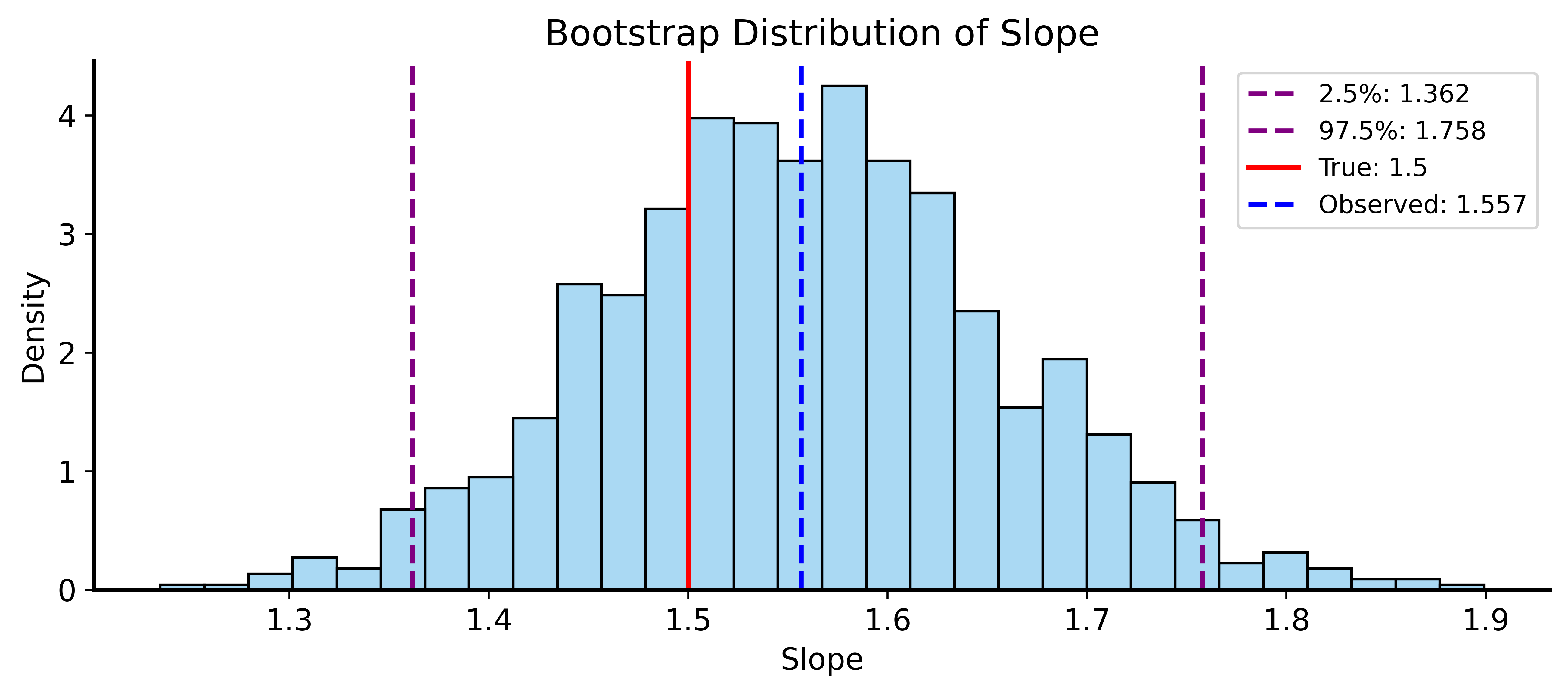
Bootstrap CI Example
Bootstrap 95% CI for slope: [1.362, 1.758]
True slope: 1.5
Parametric 95% CI: [1.352, 1.761]
Multiple Regression
What if we have multiple predictors?
\[Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_p X_p + \epsilon\]
This is multiple linear regression
The Data
| 0 |
4 |
4 |
2 |
6 |
| 1 |
1 |
1 |
2 |
6 |
| 2 |
1 |
1 |
2 |
10 |
| 3 |
4 |
2 |
3 |
15 |
| 4 |
3 |
3 |
2 |
10 |
Simple Regression: Father’s Education
OLS Regression Results
==============================================================================
Dep. Variable: G3 R-squared: 0.023
Model: OLS Adj. R-squared: 0.021
No. Observations: 395 F-statistic: 9.352
Covariance Type: nonrobust Prob (F-statistic): 0.00238
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 8.7967 0.576 15.264 0.000 7.664 9.930
Fedu 0.6419 0.210 3.058 0.002 0.229 1.055
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
But Wait…
What about mother’s education?
Let’s look at how these variables relate:
| Fedu |
1.000 |
0.623 |
0.152 |
| Medu |
0.623 |
1.000 |
0.217 |
| G3 |
0.152 |
0.217 |
1.000 |
The Problem: Multicollinearity
Father’s and mother’s education are correlated!
- Students with educated fathers often have educated mothers
- Hard to separate individual effects
Multiple Regression to the Rescue
Include both predictors:
OLS Regression Results
==============================================================================
Dep. Variable: G3 R-squared: 0.048
Model: OLS Adj. R-squared: 0.043
No. Observations: 395 F-statistic: 9.802
Covariance Type: nonrobust Prob (F-statistic): 7.01e-05
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 7.8205 0.648 12.073 0.000 6.547 9.094
Fedu 0.1176 0.265 0.443 0.658 -0.404 0.639
Medu 0.8359 0.264 3.168 0.002 0.317 1.355
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
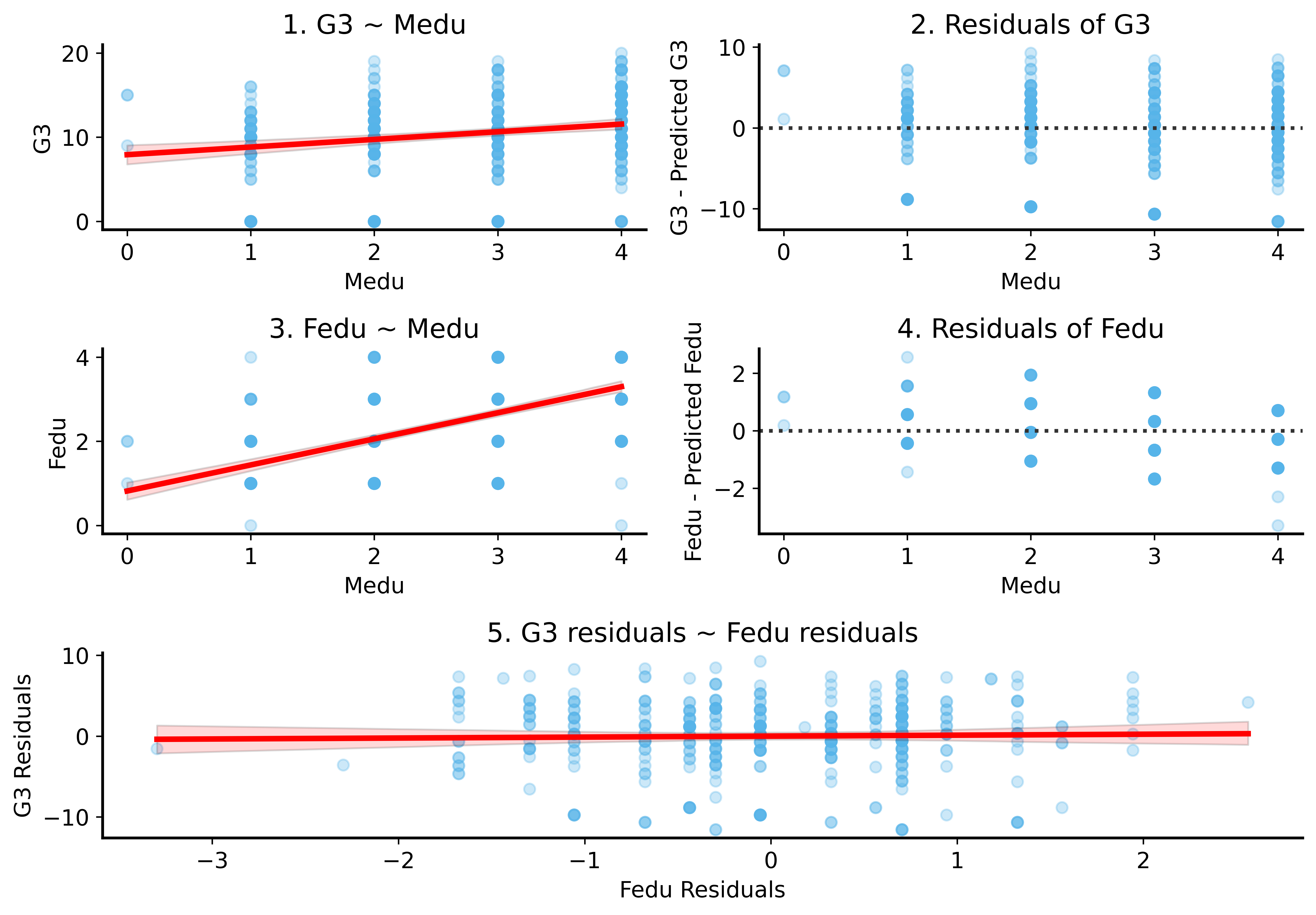
Interpretation
Before (Fedu only): significant effect
After (Fedu + Medu): Fedu effect shrinks, Medu dominates
Multiple regression controls for other variables!
Confounding Example
Does mother’s education cause better grades?
Or do they share a common cause (e.g., family wealth)?
- Wealth → can afford education for mom
- Wealth → can afford tutoring for student
The “Reverse” Regression
What if we regress Medu on G3?
OLS Regression Results
==============================================================================
Dep. Variable: Medu R-squared: 0.404
Model: OLS Adj. R-squared: 0.401
No. Observations: 395 F-statistic: 132.8
Covariance Type: nonrobust Prob (F-statistic): 9.00e-45
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.9051 0.136 6.658 0.000 0.638 1.172
Fedu 0.6080 0.040 15.319 0.000 0.530 0.686
G3 0.0299 0.009 3.168 0.002 0.011 0.048
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
This suggests G3 “causes” Medu — obviously wrong!
Summary
Regression Inference
- Use permutation tests or bootstrap for hypothesis testing
- Same principles as before, applied to regression
Multiple Regression
- Include multiple predictors simultaneously
- Controls for confounding between predictors
Causality
- Regression shows association, not causation
- Need additional assumptions or experimental design